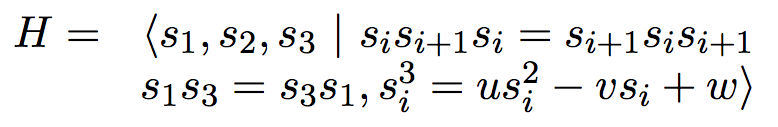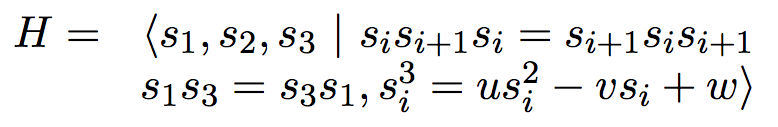Algèbre de Hecke cubique sur 4 brins
On note R = Z[u,v,w,1/w] et H l'algèbre quotient de l'algèbre
de groupe sur R du groupes de tresses à 4 brins par
les relations s^3 - u s^2 + v s - w = 0. En d'autres termes,
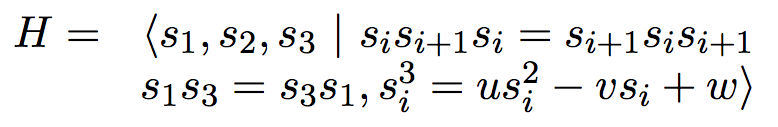
C'est par ailleurs l'algèbre de Hecke associée au groupe de réflexions complexes G25. J'ai démontré dans Cubic Hecke algebras
on at most 5 strands que H est un R-module libre de
rang 648 sur une base décrite dans le fichier baseH4.maple , avec la convention évidente
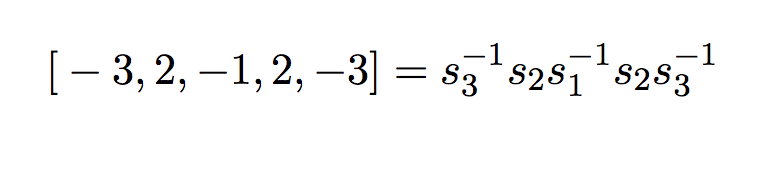 Dans les fichiers de multiplication
à gauche et multiplication
à droite on trouve les matrices des générateurs mm1,mm2,mm3 et
leurs inverses mm1I,mm2I,mm3I.
Dans les fichiers de multiplication
à gauche et multiplication
à droite on trouve les matrices des générateurs mm1,mm2,mm3 et
leurs inverses mm1I,mm2I,mm3I.
Des modèles matriciels des représentations irréductibles de H ont été obtenus par diverses personnes, notamment Broué-Malle 1993, Marin 2001 (thèse), Malle-Michel.
Dans ce fichier, u=a+b+c, v = ab+bc+ac, w = abc, et j est une racine
primitive troisième de 1.
Un quotient remarquable de l'algèbre de Hecke cubique à 4 brins
a été étudiée dans A
maximal cubic quotient of the braid algebra . On trouvera les matrices
de la structure de bimodule Q4/Q3u3Q3 sur l'algèbre de Hecke cubique à
associée dans le fichier A4tilde.gap.
Revenir à la page principale.
Revenir à la page informatique.